Merkle trees (named after Ralph Merkle, one of the fathers of modern cryptography) are fascinating data structures used in hash based data structures to verify the integrity of data in peer-to-peer systems. Systems like Dynamo use this to compare hashes – essentially itself a binary tree of hashes and typically used to remove conflicts for reads. For example – in a distributed system, if a replica node falls considerably behind its peers, using techniques like vector clocks might take unacceptable times to resolve. A hash-based comparison approach like Merkle tree would help quickly compare two copies of a range of data on different replicas. This is also a core part of blockchains like Ethereum which uses a non-binary variant but the binary ones are the most common and easy to understand and fun to implement.
Conceptually this involves:
- Comparing the root hashes of both trees.
- Continue recursion on the left and right children of the tree until the root hashes are equal.
The “Merkle root” stores the summary of all the transaction value in a singular value.
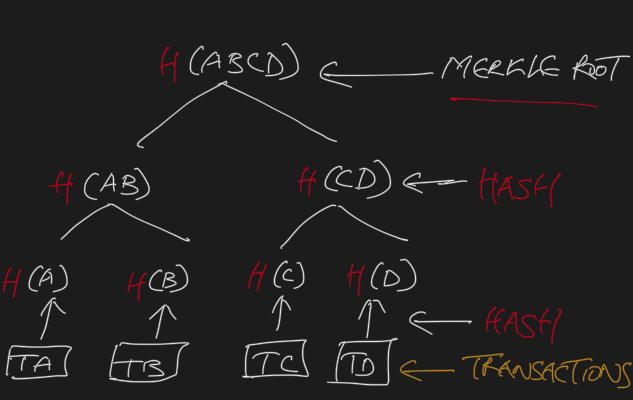
For example , if TA, TB,TC ,TD are transactions ( could be files, keys etc) and H is a Hash function. You can construct a tree by taking the transactions, hashing their concatenated values to generate children and finally reduced to a single root. In my scrawl above, this means hashing TA and TB, TC and TD, then hashing their concatenations H (AB), H(CD) to land at H(ABCD).Essentially keep hashing the until all the transactions meet at a single hash.
Example
Here’s an example that uses this technique to compare two files by generating their Merkle root to validate if they are equal of not (comments inline).
Invoke the script by calling “python merkle_sample.py “<file1>.csv” “<file2>.csv” to compare two merkle trees. Code below:
Key advantage here is that each branch of the tree can be checked independently without downloading the whole dataset to compare.
This translates to reducing the number of disk reads for synchronization though that efficiency needs to be balanced against the recalculation of the entire tree when nodes leave or go down. This is fundamental to Crypto currencies when transactions need to be validated by nodes and there is enormous time and space cost to validate every transaction which can be mitigated by Merkle trees in logarithmic time instead of linear time. The Merkle root get put into the block header that gets hashed in the process of mining and comparisons are made via the Merkle root rather than submitting all the transactions over the network. Ethereum uses a more complex variant of the Merkle, namely the Merkle Patricia tree.
The applications of this range beyond blockchains to Torrents, Git, Certificates and more.